INSTRUCTIONS: You must do at least two (2) problems from each module. Each question is worth either 1, 2 or 3 credits - . You must score at least 10 credits to complete your contract. You can do more problems to get more credits, of course.

MODULE ONE

(1) Balancing the Books  CREDITS a) You must divide 470 marbles among Bill, Mary and Anne. Bill must get 100 more marbles than Mary. Mary must get 80 more marbles than Anne. How many marbles did each person get? b) A bow and arrow cost $21. The bow costs $20 MORE than the arrow. What was the price of each?   [Help]

(2) In Stitches.  CREDITS If two stitchers can stitch two stiches in two seconds, how many stitches can six stitchers stitch in six seconds?

(3) Ten Per Side  CREDITS At a small Maori pa, in the shape of a square, there was a battle. The chief of the pa was Te Hokianga. After many days of fighting, Te Hokianga was left with just 32 men. Te Hokianga positioned his men on each side of his square pa so that each side of the pa could be defended by 10 men. a) Show how he did this. b) After the next wave of attacks, Te Hokianga had just 28 men, but was still able to have 10 men defending each side of the pa. Show how he did this. c) After the next attack, Te Hokianga lost another 8 men, but was STILL able to have 10 men defending each side of the pa. Show how he did this.

(4) Car + Breakdown = Loooong Walk!  CREDITS Sarah had bought a brand new sports car and was taking it for a spin. Three-quarters of the way through her journey, the car broke down and wouldn’t start again. With no cellphone, Sarah walked the remainder of the distance. If Sarah spent 5 times as long walking the last quarter of her journey as she did driving the first three-quarters, how much faster does she drive than walk?

MODULE TWO

(5) Apples In A Box   CREDIT There are three kinds of apples mixed up in a large box. What is the smallest number of apples could take and be SURE you have 3 apples of 1 kind?    [Help]

(6) Shoes and Socks  CREDIT I share a room with my brother. One night I went to my wardrobe to get a pair of socks and a pair of shoes. It’s quite a mess in there and in the jumble there are 6 shoes of 3 different brands, and 24 brown socks and black socks. What’s the smallest number of shoes and socks would I have to take in order to be SURE I have a pair of matching shoes and a pair of matching socks?   [Help]

(7) The Line  CREDITS The points A, B, C, D, and E are located on a straight line in order. The distance from A to E is 20cm. The distance from A to D is 15cm. The distance from B to E is 10cm. C is halfway between B and D. What is the distance from B to C?    [Help]

(8) Video Competition   CREDIT Danny’s Video is giving away a free movie to anyone who can solve this puzzle. Place the numbers one to nine in the squares so that none of the rows, columns or diagonals have the same sum. Sylvia and Brian BOTH won a free movie, each with different solutions. What were their solutions?    [Help]

MODULE THREE

(9) Tremendous Tessellations  CREDITS Create an original tessellating shape. Prove your shape actually tessellates by tessellating the shape at least 8 times. You must show ALL working, especially your original design work!	(10) Shaping the Problem 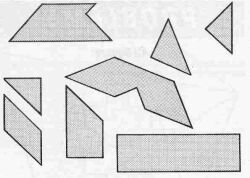 CREDIT Cut out these shapes and fit them together to form a certain letter of the alphabet.
(11) Folding the Octagon  CREDITS Create a regular octagon from a square piece of paper by using folds only and a pencil. Do not use a ruler, compass or anything else apart from a pencil and folds. 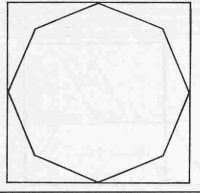Be prepared to explain how you got your solution.	(12) Ingenious Ring Linking   CREDITS Look at the three rings below. By cutting ONE ring, you can make the whole chain come apart. a) Link 5 rings so that by cutting ONE, the whole chain comes apart. b) Link 5 chains so that by cutting ANY link, the whole chain comes apart.